辞职了,散分!并改进一上汉诺塔的算法
日期:2014-05-20 浏览次数:20728 次
辞职了,散分!并改进一下汉诺塔的算法。
来公司一年多,经理就没接到什么像样的项目,大部分时间都是去支援别的项目组;我支援过测试、支援过对日外包、支援过CGI的项目、支援过.net......叫我干这些无聊的工作也就算了,经理还美其名曰“多学点东西啊,干软件的就要懂得东西多......”,我去,理由真好。唯一做过的一次JavaWeb项目,技术含量也不是很多,都是些数据库的CRUD和前台Dom的CRUD。
而且工资一直没涨,太憋屈,我就辞了。
吐槽结束。
为什么和大家一起来讨论汉诺塔呢?因为传说中,汉诺塔早在远古时期就和“世界末日”绑定在一起,今天就用这个帖子纪念我的第一次辞职和伟大的世界末日。
相信大家一定对汉诺塔有映像,我就不做过多的解释了。
以下是百度百科上的原文(http://baike.baidu.com/view/191666.htm):
一位法国数学家曾编写过一个印度的古老传说:在世界中心贝拿勒斯(在印度北部)的圣庙里,一块黄铜板上插着三根宝石针。印度教的主神梵天在创造世界的时候,在其中一根针上从下到上地穿好了由大到小的64片金片,这就是所谓的汉诺塔。不论白天黑夜,总有一个僧侣在按照下面的法则移动这些金片:一次只移动一片,不管在哪根针上,小片必须在大片上面。僧侣们预言,当所有的金片都从梵天穿好的那根针上移到另外一根针上时,世界就将在一声霹雳中消灭,而梵塔、庙宇和众生也都将同归于尽。
不管这个传说的可信度有多大,如果考虑一下把64片金片,由一根针上移到另一根针上,并且始终保持上小下大的顺序。这需要多少次移动呢?这里需要递归的方法。假设有n片,移动次数是f(n).显然f(1)=1,f(2)=3,f(3)=7,且f(k+1)=2*f(k)+1。此后不难证明f(n)=2^n-1。n=64时,
f(64)= 2^64-1=18446744073709551615
假如每秒钟一次,共需多长时间呢?一个平年365天有 31536000 秒,闰年366天有31622400秒,平均每年31556952秒,计算一下,
18446744073709551615/31556952=584554049253.855年
这表明移完这些金片需要5845亿年以上,而地球存在至今不过45亿年,太阳系的预期寿命据说也就是数百亿年。真的过了5845亿年,不说太阳系和银河系,至少地球上的一切生命,连同梵塔、庙宇等,都早已经灰飞烟灭。
我想大家一定都能理解汉诺塔的递归算法,早在谭浩强(个人认为谭浩强和严蔚敏都是计算机教育界的顶尖大师)的书上,汉诺塔递归以及斐波那契的递归是作为范例讲的;以下是Java版汉诺塔的递归源码:
用文字描述“某一趟汉诺移动”,算法是这样的:
1、对于第num个盘子的“汉诺移动”,都需要传入三个参数 盘子号num、开始柱from、借助柱with、目标柱to;
2、先把本次的from柱作为num-1个盘子的from柱,本次to柱作为num-1个盘子的with柱,本次的with柱作为num-1个盘子的to柱,对num-1个盘子进行“汉诺移动”;
3、再把本次的盘子从from柱移动到to柱;
4、然后,由于本次的盘子已经在to柱,而num-1个盘子全在with柱,所以需要把num-1个盘子从with柱借助于from柱移动to柱,即:hannoi(num-1,with,from,to)
用递归描述起来似乎很简单,但对于某些逻辑思维不强的人来说,他们还是一知半解,主要会出现以下两个疑问:
1、虽然能用程序写出来,但程序的内部是如何进行构建和运行的呢?
2、如果手边只有一张纸、一支笔,没有VisualStadio、没有Eclipse、甚至没有NotePad,如何
用最短的时间把解决步骤写出来?
下面,听我来详细解释。
一、把算法和我们接触过的模型结合起来。
仔细观察一下汉诺塔的递归算法,就会发现,它和二叉树的中序遍历基本一致。
中序遍历的文字描述:
若二叉树为空则结束返回,
否则:
(1)中序遍历左子树。
(2)访问根结点。
(3)中序遍历右子树。
Java版算法:
我记得数据结构的“划重点课”上(前面的课我都没咋去),老师曾经说过这样一句话:
二叉树的先序遍历、中序遍历、后序遍历、层序遍历四种遍历是所有树和图、所有非线性算法的基础和原理,必须牢牢掌握这四种算法的递归(层序遍历一般不递归)以及非递归;掌握不了这四种算法,就无法掌握高级的排序和查找,也无法学好下学期的算法课,写的程序就永远是入门的、线性的、低效率的。
以前我没怎么好好学习数据结构,也不太理解他的这句话,导致我以后的算法课是抄别人的抄过的,毕设也是抄的,后来又被学校推荐到了一个不太好的公司,接着后面工作无聊,辞职......看来老师说的真对。
回到我们的汉诺塔话题,结合二叉树的中序遍历,我们很容易就画出3阶汉诺塔的空间递归树:
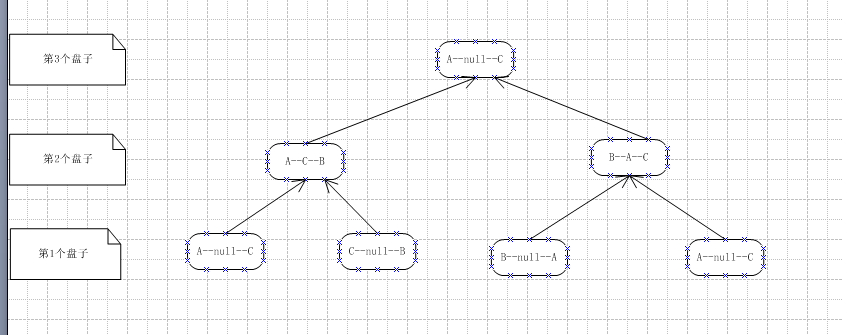
中序遍历这个二叉树,遍历某个节点时,输出from和to,with无须输出,就可以得到3阶汉诺塔的移动顺序:
盘子:1A>>>>C
盘子:2A>>>>B
盘子:1C>>>>B
盘子:3A>>>>C
来公司一年多,经理就没接到什么像样的项目,大部分时间都是去支援别的项目组;我支援过测试、支援过对日外包、支援过CGI的项目、支援过.net......叫我干这些无聊的工作也就算了,经理还美其名曰“多学点东西啊,干软件的就要懂得东西多......”,我去,理由真好。唯一做过的一次JavaWeb项目,技术含量也不是很多,都是些数据库的CRUD和前台Dom的CRUD。
而且工资一直没涨,太憋屈,我就辞了。
吐槽结束。
为什么和大家一起来讨论汉诺塔呢?因为传说中,汉诺塔早在远古时期就和“世界末日”绑定在一起,今天就用这个帖子纪念我的第一次辞职和伟大的世界末日。
相信大家一定对汉诺塔有映像,我就不做过多的解释了。
以下是百度百科上的原文(http://baike.baidu.com/view/191666.htm):
一位法国数学家曾编写过一个印度的古老传说:在世界中心贝拿勒斯(在印度北部)的圣庙里,一块黄铜板上插着三根宝石针。印度教的主神梵天在创造世界的时候,在其中一根针上从下到上地穿好了由大到小的64片金片,这就是所谓的汉诺塔。不论白天黑夜,总有一个僧侣在按照下面的法则移动这些金片:一次只移动一片,不管在哪根针上,小片必须在大片上面。僧侣们预言,当所有的金片都从梵天穿好的那根针上移到另外一根针上时,世界就将在一声霹雳中消灭,而梵塔、庙宇和众生也都将同归于尽。
不管这个传说的可信度有多大,如果考虑一下把64片金片,由一根针上移到另一根针上,并且始终保持上小下大的顺序。这需要多少次移动呢?这里需要递归的方法。假设有n片,移动次数是f(n).显然f(1)=1,f(2)=3,f(3)=7,且f(k+1)=2*f(k)+1。此后不难证明f(n)=2^n-1。n=64时,
f(64)= 2^64-1=18446744073709551615
假如每秒钟一次,共需多长时间呢?一个平年365天有 31536000 秒,闰年366天有31622400秒,平均每年31556952秒,计算一下,
18446744073709551615/31556952=584554049253.855年
这表明移完这些金片需要5845亿年以上,而地球存在至今不过45亿年,太阳系的预期寿命据说也就是数百亿年。真的过了5845亿年,不说太阳系和银河系,至少地球上的一切生命,连同梵塔、庙宇等,都早已经灰飞烟灭。
我想大家一定都能理解汉诺塔的递归算法,早在谭浩强(个人认为谭浩强和严蔚敏都是计算机教育界的顶尖大师)的书上,汉诺塔递归以及斐波那契的递归是作为范例讲的;以下是Java版汉诺塔的递归源码:
public void hannoi(int num,String from,String with,String to)
{
if(num==1){
//递归出口!
System.out.println("盘子:"+1+from+">>>>"+to);
}else{
hannoi(num-1,from,to,with);
System.out.println("盘子:"+num+from+ ">>>>" +to);
hannoi(num-1,with,from,to);
}
}
public static void main(String[] args) {
Hannoi h = new Hannoi();
h.hannoi(3, "A","B","C");
}
用文字描述“某一趟汉诺移动”,算法是这样的:
1、对于第num个盘子的“汉诺移动”,都需要传入三个参数 盘子号num、开始柱from、借助柱with、目标柱to;
2、先把本次的from柱作为num-1个盘子的from柱,本次to柱作为num-1个盘子的with柱,本次的with柱作为num-1个盘子的to柱,对num-1个盘子进行“汉诺移动”;
3、再把本次的盘子从from柱移动到to柱;
4、然后,由于本次的盘子已经在to柱,而num-1个盘子全在with柱,所以需要把num-1个盘子从with柱借助于from柱移动to柱,即:hannoi(num-1,with,from,to)
用递归描述起来似乎很简单,但对于某些逻辑思维不强的人来说,他们还是一知半解,主要会出现以下两个疑问:
1、虽然能用程序写出来,但程序的内部是如何进行构建和运行的呢?
2、如果手边只有一张纸、一支笔,没有VisualStadio、没有Eclipse、甚至没有NotePad,如何
用最短的时间把解决步骤写出来?
下面,听我来详细解释。
一、把算法和我们接触过的模型结合起来。
仔细观察一下汉诺塔的递归算法,就会发现,它和二叉树的中序遍历基本一致。
中序遍历的文字描述:
若二叉树为空则结束返回,
否则:
(1)中序遍历左子树。
(2)访问根结点。
(3)中序遍历右子树。
Java版算法:
class TreeNode{
public int data;
public TreeNode leftChild;
public TreeNode rightChild;
public static void inOrderTraversal(TreeNode node){
if(node == null){
return;
}else{
inOrderTraversal(node.leftChild);
System.out.println(node.data);
inOrderTRaversal(node.rightChild);
}
}
}
我记得数据结构的“划重点课”上(前面的课我都没咋去),老师曾经说过这样一句话:
二叉树的先序遍历、中序遍历、后序遍历、层序遍历四种遍历是所有树和图、所有非线性算法的基础和原理,必须牢牢掌握这四种算法的递归(层序遍历一般不递归)以及非递归;掌握不了这四种算法,就无法掌握高级的排序和查找,也无法学好下学期的算法课,写的程序就永远是入门的、线性的、低效率的。
以前我没怎么好好学习数据结构,也不太理解他的这句话,导致我以后的算法课是抄别人的抄过的,毕设也是抄的,后来又被学校推荐到了一个不太好的公司,接着后面工作无聊,辞职......看来老师说的真对。
回到我们的汉诺塔话题,结合二叉树的中序遍历,我们很容易就画出3阶汉诺塔的空间递归树:

中序遍历这个二叉树,遍历某个节点时,输出from和to,with无须输出,就可以得到3阶汉诺塔的移动顺序:
盘子:1A>>>>C
盘子:2A>>>>B
盘子:1C>>>>B
盘子:3A>>>>C
免责声明: 本文仅代表作者个人观点,与爱易网无关。其原创性以及文中陈述文字和内容未经本站证实,对本文以及其中全部或者部分内容、文字的真实性、完整性、及时性本站不作任何保证或承诺,请读者仅作参考,并请自行核实相关内容。
